什么是旋流器连续性和流动的数值求解？（旋流器连续性和流动的数值求解）

连续性和流动的数值求解

旋流器可用众多代表其内部位置的不同网格点来离散，用有限差分或有限单元模型来求解其控制微分方程。连续性方程用于流体、固体颗粒和动量问题，而对于不可压缩流体，则用N-S方程来描述流体运动°采用这种方法，商用计算流体力学软件包PHOENICS［Rhodes等1989］被用作预测旋流器的性能。需要输入的参数是旋流器的几何尺寸和进料流入的状态。应用此模型能预测压降、分割尺寸、级效率、流出每个出料口的流动。

当研究进口条件的改变或不同的旋流器几何尺寸设计的影响时，该模型也是非常有用的。旋流器的数值模型普遍假设沿轴向对称，它一定程度上简化了计算要求。要想真实再现悬流器内的流动状况应有三向速度的空间和时间的变化，必须允许旋流器内的湍流流动，必须适应大量固相颗粒存在以使其能代表具有粒度分布的颗粒物料。对这些变量需要很大的计算量，因此一些计算研究不得不将流动简化为层流、轴对称，甚至出口仅有一个溢流［Bloor等，1989］。 假设和限制的条目越多，结果的可靠性就越低。

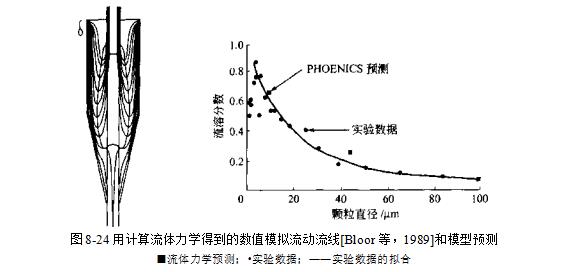
该技术提供的信息在设计和优化中具有重要应用前景，但是在训练数值模型时必须特别地注意，为了便于数学求解，数学模型中往往包含有一些阻尼因素或称“逆风”因素。特别是当建立模型时釆用的假设在物理上也不切合实际时，这可能影响结果的有效性或通用性。 因此，为了验证模型的有效性，应当进行辅助这种技术的试验验证。图8-24描述的是一个 数值研究的结果。